В статье рассматриваются подходы статистического анализа эмпирических данных полученных в результате исследования экономических процессов, протекающих в обществе. Приведен пример планирования эксперимента, предложен формат представления данных, а также порядок построения полного факторного эксперимента.

В статье рассмотрены примеры построения математических моделей носящих вероятностный характер, и проведено их исследования с помощью предложений регрессионного и дисперсионного подходов к анализу данных. Приведены примеры выводов и рекомендаций, полученных на основе исследований реальных моделей, дано краткое описание необходимых уравнений и следствий из них. Следует заметить, что представленные в статье модели носят иллюстрирующий характер, для более детального их исследования требуется более тщательная детализация.

Характерной чертой для современного уровня развития социологической и экономической науки, а также их приложений является все более широкое применение статистических методов анализа тех или иных экономических или социологических процессов. Подобные методы могут быть использованы при анализе влияния на деятельность предприятия различных факторов (внешних, внутренних) и позволяют определить их значимость. Необходимость использования этих методов связано с тем, что изучение явлений окружающего мира, становясь более глубоким, требует выявления не только основных закономерностей, но и возможных случайных отклонений от них. Наука все больше внедряется в такие области практики, где наличие и большое влияние именно случайности не подлежит сомнению, а иногда является определяющим. В настоящее время нет практически ни одной области науки, в которой в той или иной степени не применялись бы методы статистического анализа, в частности данные методы, позволяют принимать эффективные решения при проведении маркетинговых исследований предприятия.

В силу своих особенностей маркетинг требует эффективного управления [1], но те же самые особенности маркетинга делают его управление чрезвычайно трудным. Принятие решений – это выбор альтернатив. Оно предполагает наличие адекватной информации, цель которой – уменьшить неопределенность в отношении последствий принятых решений. Решение о внедрении продукта на рынок может либо повлечь за собой убытки, либо привести к росту прибыли, не менее важны исследования вопросов связанные с взаимодействие подсистем предприятия. Современная концепция управления в маркетинге состоит в том что, управление – это анализ, планирование, организация и контроль, за проведением, маркетинговых мероприятий, а ее задача заключается в воздействии на уровень, время и характер спроса для достижения целей. Статистические методы анализа данных могут с успехом применятся в социальных сферах, с их помощью можно анализировать деятельность кадровых агентств, анализировать данные предвыборных политических компаний.

Основу любой системы анализа маркетинговой информации составляет статистический банк и банк моделей. Статистический банк включает в себя совокупность современных методик статистической обработки информации, позволяющих наиболее полно вскрыть, взаимозависимости в рамках подборки данных и установить степень статистической надежности. Методики обработки информации включают методы регрессионного, корреляционного, дисперсионного, факторного, гнездового подходов к анализу математических моделей и другие математико-статистические методы позволяющие анализировать модели, носящие вероятностный характер различных областей знаний, в частности моделей деятельности предприятий. Анализ можно проводить в реальном времени, и анализировать деятельность на будущее, используя аппарат временных рядов. В начале исследования необходимо выделить значимые факторы, те явления, которые оказывают существенное влияние на модель.

Например, если с помощью регрессионного анализа исследуется влияние на прибыль Y предприятия по производству упаковочной продукции, факторов: Х1-затраты на рекламу, Х2-затраты на модернизацию производства, Х3- затраты на расходные материалы, факторов может быть сколь угодно много в общем случае по каждому из факторов набрана статистика за определенный период времени, исследованию подвергаются генеральные совокупности или выборки из них. Модели могут иметь следующий вид. Общая линейная модель будет представлена в виде [17],

(1)

модель может быть квадратичной

(2)

содержать смешанные взаимодействия факторов

(3)

где

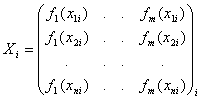матрицы наблюдений;

выборка из генеральной совокупности, данные эксперимента,

вектор неизвестных параметров в модели, e ошибка.

Уравнения 1-3, представляют собой функциональную зависимость прибыли Y от факторов . В качестве функций могут выступать любые непрерывные функции, например экспонента или логарифм, их выбор зависит от конкретных эмпирических данных, априорной информации.

Далее следует процедура оценки неизвестных параметров , обычно оценку проводят с помощью метода наименьших квадратов (МНК) [11]. Рассмотрим метод наименьших квадратов в свете того, что он, по сути, является частным случаем метода максимального правдоподобия. В методе также приходиться решать оптимизационную задачу, искать минимум специальной функции, которая строится следующим образом, формула

(4)

где

– функция распределения,

- эмпирическая функция распределения.

Вычисление оценок МНК не требует, вообще-то говоря, введения каких-либо дополнительных гипотез. Сам метод часто рассматривают как способ «разумного» выравнивания эмпирических данных. Однако судить об адекватности модели, об ее прогностической способности удается лишь за счет введения априорных сведений, зафиксированных в предпосылках классической регрессии. Вообще говоря, просто оценить параметры недостаточно, необходимо, что бы полученные оценки обладали свойствами несмещенности, эффективности и состоятельности [10]. Итак, в результате проведения оценки параметров регрессионной модели получены значения вектора оценок параметров . Теперь уравнения 1-3 подставляем в виде, соотношение 5,

(5)

Теперь оцененную модель можно использовать для прогнозирования прибыли, взяв в качестве значений факторов желаемые значения. На основе проведенного анализа делаются выводы, предлагаются рекомендации, приведем пример.

Если на рекламную компанию тратить менее 24 тысяч рублей в месяц, то увеличение объема производства влечет за собой увеличение убытков. Следовательно, на рекламу нужно тратить больше 24 тысяч рублей. Реклама вносит наибольший вклад в прибыль. Увеличение расходов на модернизацию, влечет за собой увеличение прибыли. Сумма по всем трем факторам будет ограничиваться предыдущей прибылью. Так как параметр при факторе - расходы на рекламу имеет наибольшее значение, следовательно, для развития предприятия в данный момент времени приоритетным является увеличение расходов на рекламу. Распределение оставшейся части денег между модернизацией и затратами на расходные материалы будет определяться количеством затраченных денег на рекламу, а также объемами производства и возможностью проведения модернизации. Выводы сделаны на основе реальных эмпирических данных, при исследовании модели предложенной в уравнениях 1-3. Необходимо отметить, что при построении модели факторы должны носить количественный характер (рубли, килограммы и т.п.).

Если факторы в модели носят качественный характер (штуки, люди, количество чего либо и т.п.) то удобно применять методы дисперсионного анализа, пусть мы исследуем модель, описанную уравнением 1, в котором положим;

- вектор значений отклика,

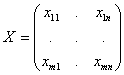- матрица наблюдений (значений) соответствующих факторов, - вектор неизвестных параметров, - вектор ошибок измерений. При построении модели необходимо четко представлять, сколько факторов мы используем и сколько уровней имеет каждый фактор, например для исследования мы выделили три фактора это возраст, образование и пол людей приходивших в кадровое агентство с целью поиска работы, каждый фактор был представлен уровнями

Таблица 1 − Смысловое представление модели «Кадровое агентство»

Фактор	Уровень 1	Уровень 2	Уровень 3
Возраст	20-30 лет	30-40 лет	40-50 лет
Образование	Общее	Среднее специальное	Высшее
Пол	Мужской	Женский

После этого по каждому уровню всех факторов необходимо набрать статистику, для составления плана эксперимента, для более полного и качественного анализа необходимо составить полный факторный эксперимент (ПФЭ). ПФЭ это всевозможные комбинации уровней факторов. Далее проводим оценку параметров, учитывая то, что матрица , в общем случае имеет дефект ранга, следовательно, придется использовать метод псевдообращения матриц, необходимо решить следующую систему уравнений [16],

(6)

откуда получаем

(7)

где , z- произвольный вектор.

Таких оценок, вообще говоря, бесконечность и такие оценки являются смещенными, но существуют линейные комбинации вида , для которых оценки являются несмещенными, такие оценки называют функциями допускающими оценку (ФДО). ФДО также бесконечность, но существует базис, относительно которого можно построить любую ФДО. Для ПФЭ можно априорно предложить базис ФДО и преобразовать модель к модели полного ранга, применяя следующую процедуру.

Пусть матрица наблюдений соответствующая ПФЭ, с числом наблюдений , где - число уровней фактора . Проведем факторизацию матрицы наблюдений , выполнив преобразование

(8)

где матрица размерности обладает полным рангом по столбцам,

матрица размерности обладает полным строчным рангом.

При этом уравнение наблюдений преобразуется к виду 9,

(9)

где - вектор ФДО. Модель 9, будет моделью полного ранга, которую рекомендуется взять в качестве исходной.

После проведения анализа с помощью дисперсионного анализа, для модели представленной в Таблице 1, получили например следующие выводы и предлагаем рекомендации.

1) В результате анализа установлено, что на отклик существенно (значимо) влияет фактор X2 (образование). Парные взаимодействия факторов не оказывают существенного влияния на результат эксперимента. Остаток значим. Это свидетельствует о том, что выбранная модель неадекватно описывает экспериментальные данные и нуждается в уточнении.

2) Установлено, что на отклик существенно (значимо) влияет фактор X2 (образование). У фактора X2 (образование) значимо различаются эффекты уровней 1 (общее образование) и 3 (высшее образование), 2 (среднее образование) и 3 (высшее образование), причем уровню 1(общее образование) соответствует наибольшее среднее значение отклика, а уровню 3 (высшее образование) - наименьшее среднее значение отклика.

Различие между эффектами других уровней незначимо.

3) Наибольшее среднее значение отклика наблюдается на 1 - м уровне фактора X2;

наименьшее среднее значение отклика наблюдается на 3 - м уровне фактора X2; влияние остальных факторов несущественно, т.е. различие между средними значениями отклика для различных уровней этих факторов незначимо. Уровни фактора X2 в порядке убывания среднего значения отклика образуют последовательность: уровень 1 (общее), уровень 2 (среднее специальное), уровень 3 (высшее).

Результаты были получены исходя из реальных данных кадровых агентств.

Сделаны следующие выводы:

Необходимо дополнительно уточнять данные эксперимента, проводить исследования более длительный период, используя статистику по нескольким агентствам одновременно.

Выяснилось, что наиболее существенное значение оказывает фактор 2 (образование), чаще всего в агентства обращаются люди, имеющие только общее образование, они чаще всего ищут временную работу. Рекомендуем организацию курсов обучения и последующего трудоустройства данной категории граждан. Другие факторы возраст и пол оказывают слабое влияние на предложенную модель.

Цель статистического анализа в том, чтобы, минуя слишком сложное, зачастую практически невозможное исследование отдельного случайного явления, обратится непосредственно к законам, управляющими массами таких явлений. Изучение законов позволяет осуществлять прогноз в области случайных явлений и целенаправленно влиять на ход таких явлений, контролировать их, ограничивать сферу действия случайности, сужать влияния случайности на практику, решать практические задачи управления и контроля предприятия.

Перед исследователем, применяющим статистический подход при проведении маркетинговых исследований, ставятся задачи описания явлений, анализа и прогнозов, выработка оптимальных решений. Во время решения возникающих задач необходимо использовать соответствующее программное обеспечение, что позволят существенно увеличить объем и сложность обрабатываемой информации, при этом быстро и своевременно получать необходимые данные, делать выводы, принимать решения, опережая конкурентов.

Несмотря на то, что необходимость применения статистических методов исследования велика, имеется много разработок в области прикладного программного обеспечения для их реализации, в частности подобные пакеты программ разрабатываются специалистами в области прикладной математики. Следует заметить, что подобные методы на практике используются редко, так как требуют некоторой специальной подготовки специалистов экономического профиля различного уровня.

Рекомендуемая литература

1. Виханский О.С., Стратегическое управление. - М.: Изд-во МГУ, 1995.

2. Кинг У., Клиланд Д. Стратегическое планирование и хозяйственная политика. - М.: Прогресс, 1982

3. Маркова Е.В., Денисов В.И., Полетаева И.А., Пономарев В.В. Дисперсионный анализ и синтез планов на ЭВМ. – М.:Наука,1982.

4. Шеффе Г. Дисперсионный анализ. – М.:Физматгиз,1963.

5. Хикс Ч. Основные принципы планирования эксперимента. – М.:мир,1967.

6. Рао С.Р. Линейные статистические методы и их применение. – М.:Наука, 1968.

7. Браунли К.А. Статистическая теория и методология в науке и технике. – М.:Наука,1977.

8. Денисов В.И., Полетаева И.А., Хабаров В.И. Экспертная система для анализа многофакторных объектов. – Новосибирск.: НЭТИ,1992.

10. Лемешко Б.Ю. Статистический анализ одномерных наблюдений случайных величин – НГТУ Новосибирск 1995. – 125с.

11. Лемешко Б.Ю. Курс лекций по методам оптимизации – НГТУ Новосибирск 1999.

12. Кокс Др., Оукс Д. Анализ данных типа времени жизни.

13. Крамер Г. Математические методы статистики. – М: Мир 1975. – 648с.

14. Кендалл М., Стюарт А. Статистические выводы и связи. – М: Наука. – 900с.

15. Губарев В.В. Вероятностные модели: Справочник. В 2-х ч. НГТУ – Новосибирск, 1992. – 422с.

16. Денисов В.И., Попов А.А. Условия оптимальности в алгоритмах в сингулярном планировании. Межвузовский сборник научных трудов. Применение ЭВМ в оптимальном планировании и проектировании. – Новосибирск 1981.- 199с.

17. Попов А.А. Курс лекций по статистическим методам анализа данных- НГТУ Новосибирск 1999.